Cho hai số phức z1 ,z2 thỏa mãn |z1-5+3i|=|z1-1-3i|, |z2-4-3i|=|z2-2+3i|. Giá trị nhỏ nhất của biểu thức...

Question

Cho hai số phức \(z_{1} ,z_{2}\)  thỏa mãn \(\left|z_{1} -5+3i\right|=\left|z_{1} -1-3i\right|, \left|z_{2} -4-3i\right|=\left|z_{2} -2+3i\right|\). Giá trị nhỏ nhất của biểu thức \(P=\left|z_{1} -z_{2} \right|+\left|\overline{z_{1} }-6+i\right|+\left|z_{2} -6-i\right|\) là

\(A. \frac{16}{\sqrt{13} } . \)

\(B. \frac{18}{\sqrt{13} } . \)

\(C. 2\sqrt{10} . \)

\(D. 6.\)

Answer 1

Chọn B

Đặt \(z_{1} =x+yi\)

thì \(\left|z_{1} -5+3i\right|=\left|z_{1} -1-3i\right|\Leftrightarrow 2{\rm x}-3y-6=0\left(d_{1} \right).\)

Đặt \(z_{2} =x'+y'i\) thì

\(\left|z_{2} -4-3i\right|=\left|z_{2} -2+3i\right|\Leftrightarrow {\rm x'+3}y'-3=0\left(d_{2} \right).\)

Gọi A, B lần lượt là điểm biểu diễn của \(z_{1} ,z_{2}\)  

thì \(A\in d_{1} ;B\in d_{2} .\)

Gọi \(C\left(6;1\right).\)

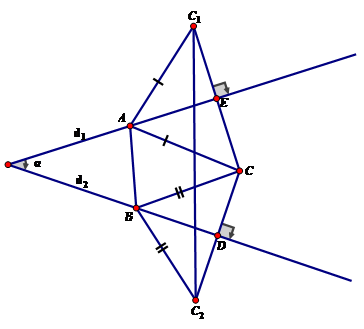
\(\begin{array}{l} {P=\left|z_{1} -z_{2} \right|+\left|\overline{z_{1} }-6+i\right|+\left|z_{2} -6-i\right|} \\ {=\left|z_{1} -z_{2} \right|+\left|z_{1} -6-i\right|+\left|z_{2} -6-i\right|.} \\ {=AB+AC+BC\ge C_{1} C_{2} .} \end{array}\)
Với \(C_{1} ,C_{2}\)  lần lượt đối xứng với C qua \(d_{1} ;d_{2} .\)

Phương trình \(CC_{1} :{\rm 3x}+2y-20=0\Rightarrow C_{2} \left(\frac{66}{13} ;\frac{31}{13} \right)\)

Phương trình \(CC_{2} :{\rm 3x-}2y-16=0\Rightarrow C_{2} \left(\frac{24}{5} ;\frac{-13}{5} \right)\)

Vậy \(C_{1} C_{2} =\frac{18}{\sqrt{13} } .\)