Chọn A
Giả sử M, N lần lượt là điểm biểu diễn của số phức z1 và z2
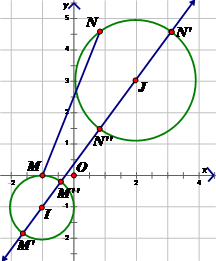
\(
\left|z_{1} +1+i\right|=1\Rightarrow M\in \left(I;1\right),\quad I\left(-1;-1\right)
\left|z_{2} -2-3i\right|=2\Rightarrow N\in \left(J;2\right),\quad J\left(2;3\right)\)
\(P=\left|z_{1} -z_{2} \right|=MN\)
Ta thấy hai đường tròn (I) và (J) nằm ngoài nhau. Do đó
\(M''N''\le MN\le M'N'.\)
\(P=\left|z_{1} -z_{2} \right|=MN\) đạt giá trị nhỏ nhất khi và chỉ khi \(M\equiv M'',N\equiv N''\)
\(P_{\min } =IJ-R-r=2,\quad P_{max} =I+R+r=8.\)